Trading or Gambling? A Quantitative Answer
And the rational case for bold bets regardless
If you are returning to this article, I have made important edits for correctness and/or clarity.
When I was young, people called me a gambler. As the scale of my operations increased I became known as a speculator. Now I am called a banker. But I have been doing the same thing all the time.
Sir Ernest Cassel
Finance is a steaming melting pot of risks and opportunities constantly being served to investors and traders everywhere to partake as much as their risk appetites and wallets can allow. Each expenditure is beneficial or costly with no forewarning, compelling participants to act solely based on their best guesses while hoping for overall benefit. When is it trading or investing, and when is it gambling? It sounds trivial, but it’s an age-old question that is difficult to answer because when risk is involved, outcomes alone do not distinguish skill from luck, and to further complicate things, skill and luck often do intersect.
So far, attempts to make this distinction often involve scanning a trader’s behavior for several of the gambling symptoms listed in the DSM. But this isn’t satisfactory. Firstly, trading and gambling are eerily similar and the higher the risk, the more luck affects the outcome, making it harder to tell the difference. Secondly, this process isn’t really suitable for self-assessment since it requires self-awareness and introspection which are not universal human traits. Finally, by the time gambling symptoms are noticeable, the financial and psychological damage are usually quite severe. The investment community needs to find a better way to tell and my thinking led me to a tentative quantitative framework.
What we’ll go over:
A universal definition of risk for all risk appetites
To what extent are trading and gambling the same
A mathematical framework to distinguish them
The four types of edge as revealed by the framework
Why position sizing is not a risk consideration per se
How to size bets to promote good trading psychology and discourage gambling
The mathematical case for bold bets even when and especially if you are gambling
The typical dictionary’s definition of risk is the chance that something bad happens. It’s a nice simple definition for everyday life, but it implies that choices and their outcomes are simple. Presented with a risk, you either take the chance or you don’t, and there after, the bad thing either happens or it doesn’t.
We can describe this mathematically. In mathematics, whenever you hear simple think of indicator functions ( an indicator function is a function that takes some input and gives you 0 or 1 as output). Indicator functions are god-tier because they allow you to very precisely shape the output of more complicated functions. Say you have a big, scary function f(x) defined on large (possibly infinite) or ‘unwanted’ domain and you only care about the function’s behavior on a very specific sub-domain A. All you need to do is multiply an indicator function to f(x).
1A(x) is the indicator function that gives 1 if x is inside A and 0 if not. Apologies if this is too abstract. Let me use an example. Think of an options payoff. It depends on what the strike (K) and underlying’s price (S) are. So you could say for call options, the sub-domain you care about is A = S>K and for put options A=S<K.
With this in mind, let’s go back to the dictionary definition of risk. Suppose A is the event take the risk and B the event bad thing happens. Mathematically, the outcome is
This function is what someone implies when they think like this:
This is the wrong way to think about risk. At the very least, we know that risk is a chance. The kid in the post (or anyone who thinks this way) assumes that the chance itself—the probability of the event happening—either exists or it doesn’t, which is different from thinking that the event either happens or doesn’t. It’s a subtle difference, but a crucial one because it reflects the perspective from which you are looking at things. The question of whether chance itself exists or not is like asking ‘Has the uncertainty been resolved?’. Since you can only answer this in hindsight, then the flaw in the kids thinking is that he assumes knowledge you can only have once the outcome is certain (ex-post) is a knowable fact before the affair is settled (ex-ante).
Author’s note: For those who care about the probabilistic explanation. Any random variable, regardless of its probability distribution and regardless of whether this distribution is continuous or discrete, collapses to a Bernoulli trial upon realization i.e. the event either occurs or does not. So all random variables are, ex-post, the same as a single instance of a Bernoulli distribution with the space {0, 1}, X ~ Bernoulli(p). But p is still determined by the random variable’s original distribution. So the only mistake the kid makes is assuming p=0.5 always. In other words, he thinks that since the thing either happens or it doesn’t, we are certain that the outcome is binary which should mean the probability of either outcome is equal (1/2). But, even though we are certain that there are two final outcomes, we don’t know their probability and can only infer them from the random variable’s probability distribution before it collapses to a Bernoulli trial. In short, he assumes knowledge you can only have ex-post as an ex-ante fact. (See video below)
Framed this way it sounds very stupid, but you will find it among people who should know better. Gambler’s often think things like: “I almost won last time. I’m likely to win this time.” or, “The last five coin flips have been heads, the next one is surely tails”. It’s a phenomenon known as the Gambler’s fallacy. In fact, you can define all of gambling by this process of substituting resolved uncertainty for ongoing uncertainty. In gambling, your concern is with the probability that you win and don’t win a bet, the bernoulli trial, rather than the probability distribution that tells you which choice would make you a winner. It is as if you believe you know the future outcome of a risky event for sure—a godlike certainty that inspires godlike feelings… until reality hits. You skip the latter mentally; the part where the real risk exists. In this sense, either you never actually consider the risk but instead consider the ex-post outcome as fixed based on a set of subjective and incomplete assumptions, or you take your model of the risk event’s dynamics and impose your subjective assumptions of the probabilities to arrive at a post-event (ex-post) state, before the event(ex-ante) happens.
Wait… read that again “…or you take your model of the dynamics of the risk event and impose your subjective assumptions of the probabilities to arrive at a post-event state before the event has happened” Isn’t this how risk management is taught? Isn’t that what the professionals do? Yes. So the difference between gamblers and professionals is that the latter guess their probabilities in a sophisticated way? Yes. Basically this meme.
The uncomfortable truth is that professional risk management and gambling are the exact same process—assigning subjective probabilities to future outcomes. Continuing with the analogy of the reddit kid, the kid assumes all outcomes are 50/50, a risk manager tries to guess better 50 is more likely by focusing on the distrubution of the random variable when the uncertainty in ongoing—when the risk is active.
It is said that the line between trading and gambling is incredibly thin. But, it does exist! If we can define it, we can have a clear heuristic to know when we are gambling and when we are trading/investing. This is important because to the extent that you are not gambling and are actually trading or investing, you have a higher chance of being profitable. Besides, a whole career path—risk management—depends on where this line is.
Let’s be a bit lenient and call gamblers ‘naive risk managers’, so that we can simply call this process of arriving at subjective probabilities risk management. Let’s then go back to our definition of risk: risk is the chance of something bad happening. Both naive risk managers and professional risk managers (henceforth professionals) want to minimize this chance by estimating probabilities as close to their true but unobservable ex-post values. This introduces a new risk (that is independent from the event risk)—the chance that you are wrong. Gamblers assume they are right, assigning a probability of 0 so in their minds this risk event collapses to a resolved state. Professionals also estimate this probability and use it to update their probability estimates for the main risk event. If they think they are far from being right, they recalculate their probabilities and update their previous event risk probabilities if the new probability that they are wrong is lower. This reiterative process is the sophistication layer that distinguishes the professionals from the gamblers.
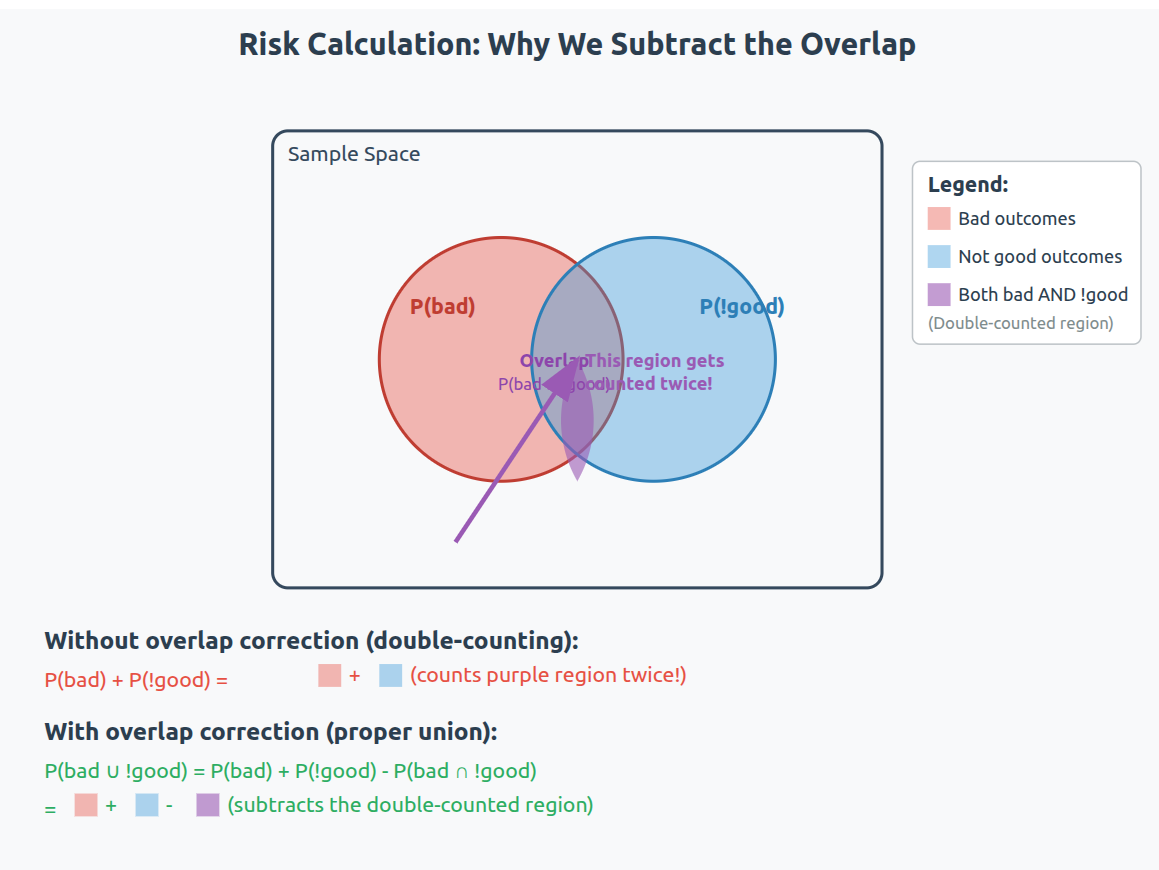
But we still haven’t found the line that distinguishes pros from gamblers. The problem lies with our definition of risk. Hitherto, we have been concerned with the chance that something bad will happen. mathematically, we have operationalised this as best as we could. If we want to go further, we need to redefine risk. Let’s try to modify the definition without changing it. How about: risk is the chance that something good will not happen? While this definition sounds purely semantic, it isn’t complete because the opposite of something bad happening is not something good not happening. For example, if I tell one person ‘the driver didn’t crash the racecar’ and another person ‘the driver didn’t win the race’, I haven’t relayed the same exact information. To convey the exact same message, I need both statements: 'The driver didn’t win the race and he crashed the racecar'. The combined statement contains the full information we want to convey and it brings some added benefits you will see later.
Formally, we have gone from risk = P(bad) to :
We now have two perspectives. A defensive one that focuses on minimizing loss ( P(bad)) and an aggressive one that focuses on minimizing lost opportunity (P(!good)). The reason this is a better definition of risk is because it recognizes that the existence of risk implies opportunity, otherwise there’s no reason to even think about taking the risk. The default behavior on encountering risk would be to completely avoid it, which is what the original definition implies you should do. Our new definition provides context. We cannot decide whether to take a risk without context. But is this definition for everyone? Yes. Say you are an extremely risk averse agent, maybe you are selling puts. You only care about P(bad) = P(payout a lot of money). Your only benefit is the premium so P(good) = P(get premium). But P(!good) = P (don’t get premium) = 0 (you are paid upfront) and our new definition collapses to the original one. If, on the other hand, you are extremely risk seeking, like say an F1 driver. Then P(!good)= P(don’t win race) and P(good) = P( win race). Since there can only be one winner, P(!good) is 19/20 or 95% so that P(!good) = 1 - P(good) = 1 - P(win). Also, P(bad) = P(crash and injured/die) so risk = P(bad) + P(!good) - P(bad).P(!good) = P(crash and die) + P(don’t win) - P(crash and injured/die).P(don’t win). Since you are good enough to be in F1, and there are safety measures put in place and all sorts of in-race safety procedures, we can assume that P(crash and injured/die) is in general very small, so that you only need to minimize P(don’t win)—to reduce missed opportunities. Our definition therefore allows you to define risk regardless of a risk-taker’s appetite. It proves that risk itself is objective and is based on the context. If you can’t completely define the context, what you have is not risk, it is uncertainty and therefore cannot be managed. But, even though risk is objective, risk perception is not, and the unobservable nature of risk makes risk management purely subjective. In other words, despite your best efforts, you are still guessing.
Risk is not directly observable. Even ex-post, when you know the outcome, you can’t say anything what the risk really was. This is an important concept to internalize. Remember the Gambler’s fallacy and how gambler’s substitute ex-post knowledge for ex-ante facts? A lot of quantitative finance does this too! Volatility estimates are often based on past volatility assuming it predicts future volatility; All quantitative strategies are based on the idea that past patterns will repeat; Backtesting is done with the assumption that a good Sharpe will carry on into the future; Monte Carlo simulations generate distributions by obtaining parameters from past returns; Portfolio optimization assumes that past average returns and average volatility will continue on; Factor models assume that past factor loadings will persist into the future. In other words, the most sophisticated tools we have are still subjective and therefore not fundamentally superior to a random guess (gambling). Why then bother at all?
What makes the difference, and what makes all the modeling worth it, depends on a small but crucial change to our definition of risk. Right now, we have that:
The term P(bad and !good) prevents us from double-counting the overlap.
If there is no overlap i.e. the two events that define risk are independent, then P(bad and !good) = 0. If they are dependent, then P(bad and !good) gives the interaction between the two events and it is removed from the joint distribution because the joint distribution will already have this information due to implicit conditional probabilities. In simpler words, if the events are dependent, then P(bad) and P(!good) are just P(bad| !good) and P(!good|bad), and P(bad and !good) removes the overlap. The term P(bad and !good) can be rewritten as P(bad) * P(!good | bad), so we can update our definition of risk to:
Note that the last two equations are equal; you can flip the conditional probabilities. This definition changes everything!
What the definition implies is that the moment we know one of the events, we get a more accurate estimate of the joint probability; of the risk. Our probability estimates then become better than those of a gambler. How do we know? Remember when we introduced the risk we were wrong aka model risk? The conditional probabilities mean that once something becomes known, we can say for sure that we have minimized model risk. Even if the realized outcomes eventually favor the gambler, our process was superior because as we learnt new information, we updated our probabilities towards the true ones, and therefore had superior guesses. We have an idea of what we know and what we don’t know and our perception of risk moved closer to reality.
We are getting closer to our line.
Our risk function assumes that risk doesn’t change, but in finance and other games of chance, risk is dynamic. We need to think about risk(t), where t is some chronological index like time. We therefore need:
As time moves along, we get to check if a conditional event has happened. We can therefore redefine the function using indicator functions so that we can take advantage of the chronological nature of time. Let’s say that X = 1 if the bad event occurs, and X=0 if not. Instead of P(bad) we have E[X] = P(bad). Instead of asking “What is the chance that something bad happens?”, we are asking “Do we expect something bad to happen or not?”. At any point in time t, we can consider all the available information that tells us if X can happen or not—the sigma-algebra Ft. Since time is chronological, we the filtrations F0⊆F1⊆F2⊆⋯FT. Even though our filtrations are indexed by time t, ‘time’ simply means when the information is published, or when you find out. The +1 then doesn’t mean ‘the next day’ or ‘the next interval’, it means ‘the next time there’s new info’. This allows us to model dynamic risk that is ‘fixed’ like the results of a sports game. Each new point in time either introduced new relevant info or not thus equating the new sigma-algebra to the previous one. F0 means we know nothing (or time hasn’t started) so E[X |F0] = Pt(bad | F0) = P(bad). We are therefore interested in estimating E[X |Ft] = Pt(bad | Ft)—we want to find out what is the right guess not what is the right outcome!
E[X |Ft] is a special kind of process called a martingale which we can denote as Mt. Martingales are such that E[E[X |Ft+1] |Ft] = E[X |Ft]. This just means that once you know all there is to know, your best guess today will be your best guess tomorrow unless there is new information—there is no hidden edge in the information. Why ? Because any exploitable information asymmetry is quickly eliminated. New information spreads to everyone quickly causing prices to adjust almost instantaneously to reflect currenly available info. No one can learn something from the available information that others haven’t already gleaned and priced in, so markets won’t move until there is new information. Margingales converge to the outcome (Doob martingale convergence theorem) :
Since F0⊆F1⊆F2⊆⋯FT, and our expectations updated as new information comes out, our expectations improve in accuracy. Therefore, you will converge to the correct expectations as you consume new information and refine your guess. And this happens before you know the outcome!
Our risk function becomes:
or in martingale form:
We can now say that the line we are looking for exists and where it is. If the outcome becomes fully known at time T, then there exists a point in time where all the available information at your disposal can give you a close enough guess. At that point, your estimates of the probabilities involved are close enough to reality for you to be generally right about things. You have an edge.
We therefore have a clear line to distinguish naive risk management (gambling) and professional risk management (trading/investing). You are gambling if you decide based on insufficient information required to make the right guess that can be made from the available information (whether or not you win or lose). The problem is that you can’t tell whether you’ve crossed it or not i.e. whether you have absorbed sufficient information to make the right guess. You therefore have to consume as much of the available information as you can and make your best guess.
Is this definition is robust enough to fully distinguish gambling from professional risk-taking? Yes. There are only three ways you can be insufficiently informed to make a good decision. Either you have all the data but not all the information because you didn’t gather all the information available from the data (incorrect interpretations due to biases, for example), you haven’t obtained enough data to be adequately informed, or you act before there enough data available (impatience or you misjudged how much you needed to know). There are therefore only three core sources of edge: superior data gathering (knowing what others don’t), unbiased assessment (correct interpretation of the data), and optimal timing of decisions relative to information arrival. And this assumes everyone has perfect analytical skills (no one can read the data better than others). This isn’t true of course so you have to add experience/education as another source of edge. Trader’s who learn from their mistakes outperform those who don’t.
The general who wins makes many calculations in his temple before the battle is fought
Sun Tzu
Our line between gambling and professionalism is agnostic to bet size. You are not gambling simply because are staking a large portion of your capital. This is why the magnitude of one’s profits or losses says nothing about their skill. But bet size can compromise the quality of your decision-making, which is why you should decide on the bet size after you’ve decided whether to take a risk. You will be more risk-averse if you stand to lose a lot, making you more sensitive to P(bad), and more risk-seeking if you stand to gain a lot, making you more sensitive to P(!good). This distortion can prevent you from making the right guess, so you want to size your bet to compensate for your sensitivity to risk and push you back to neutral. Since the bad event is the one that causes harm, you can improve your decision making by making yourself more sensitive to losses (P(bad)) than missed opportunities (P(good)). This is why you should generally bet as big as your risk limit allows. If you stand to lose a lot, you will avoid gambling.
In fact, a paper by mathematician Kyle Siegrist showed that when faced with unfavorable odds, you would be better off making bold bets even though you could potentially lose everything very quickly. Timid bets guarantee ruin, but bold bets have a chance. In fact, depending on how much you start with, you can vary your bet size based on things like how much you have left, or how close you are to your target, leading to infinite variations of the optimal strategy.
With timid play, the gambler makes a small constant bet on each game until she is ruined, or reaches the target. This turns out to be a very bad strategy in unfair games, but does have the advantage of a relatively large expected number of games. If you play this strategy, you will almost certainly be ruined, but at least you get to gamble for a while.
With bold play, the gambler bets her entire fortune or what she needs to reach the target, whichever is smaller. This is an optimal strategy in the unfair case; no strategy can do better. But it is very quick! If you play this strategy, there’s a good chance that your gambling will be over after just a few games (often just one!).
CAVEAT!
Amazingly, bold play is not uniquely optimal in the unfair case. Bold play can be rescaled to produce and infinite sequence of optimal strategies. These higher order bold strategies can have large expected number of games, depending on the initial fortune.
From Siegrist, K. (2008). How to gamble if you must. AMC, 10, 12.
So whether you are gambling or trading/investing, it is optimal to size as big as possible.
Feedback and criticism are welcomed.
Share with a fellow degenerate
This is one of the most beautiful pieces of music I’ve ever heard.